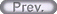３．２　電気単極と磁気単極

　前節の仮定のように点電荷を同心球面対共振回路の内球面の表面電荷と捉えてみる。電荷のプラスとマイナスは同じ実体で位相が180度異なる二つの状態といえる。電荷の時間変化によって相対的に電流荷が生じる。これもプラスの状態（放射）とマイナスの状態（吸収）が存在する。

　ところで、式(5b)によれば磁界 H の回転がゼロであるから、 H はスカラー関数 φ_m(r) を用いて、式(11) と表される[4]。

(11)

ここで φ_m は磁気ポテンシャルであり、放射状の磁界が内在していることを示している。すなわち、ここでいう電流荷が磁荷と呼びたいものの正体であろう。

　この場合、電荷も磁荷（電流荷）も1点を共有する‘一つのもの’の別状態である[5]。プラスとマイナスの電荷を別々の独立存在として、つまり電気単極の存在を認めるなら、プラスとマイナスの電流荷、すなわちN極とS極の磁気単極の存在も認めてよいだろう。逆に磁気単極の存在を認めなければ電気単極の存在理由も説明できないであろう。もっとも磁気単極は未だに観測されていない。ディラックの予測によれば電荷の離散性を説明するのに磁気単極の存在が不可欠であるという[6]。逆にいえば、磁気単極が観測されないような世界に私たちが住んでいるが故に、電気単極がだけが存在するように見えているのだともいえる。

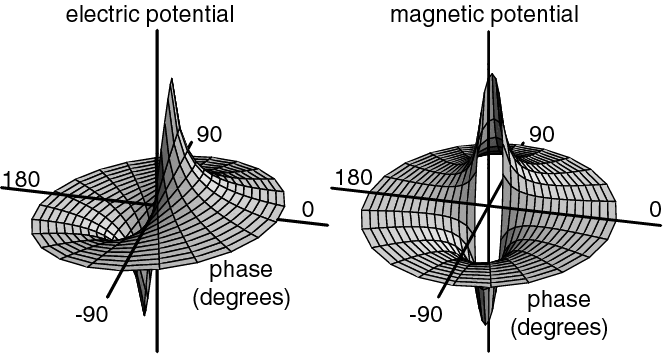
　図７に電荷と磁荷の位相変化を表すモデルを示し、図８に複素点電荷の電気および磁気ポテンシャルの位相相関図を示す。

（1999年10月6日受理）

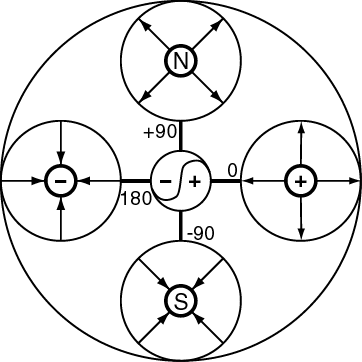
図7　電荷と磁荷の位相変化モデル
Fig.7 Phase transformation model of a pair of electric and magnetic charges.

図8　複素点電荷の位相−ポテンシャルモデル
(a) 電気ポテンシャル　(b)磁気ポテンシャル
Fig.8 Phase-potential model of dual essentialities of electric pole.
(a) Electric potential (b) Magnetic potential