２．３　同心球面対共振回路

　大小二つの球面を考える。図５のように、それぞれの半径を a , b ( a < b ) とし、球の中心は互いに一致するものとする。

図5　同心球面対共振回路
Fig.5 A resonance circuit with a pair of concentric spherical surface.

球面をコンデンサの電極面ととらえ、キャパシタンスを C とする。また両球面間の空間はインダクタンス L をもつと考える。この同心球面対は LC 共振回路とみなすことができ、その共振周波数は、式(6a)で表される。

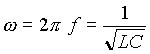(6a)

さらに式変形すると、共振周波数は内径 a と外径 b の相乗平均に逆比例することを示す式 (6b) を導くことができる[2]。なお、 c は光速を表す定数である。

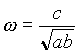(6b)

　一般に電束というのは、始点に正の電荷が、そして終点に負の電荷が存在する。球対称の電束場を考えるにおいて、内側から外側に向かう方向を電束の正の方向とすれば、内面 ( r=a ) には電束密度に相当する正の表面電荷（表面電荷密度）が生じる。一方、外面 ( r=b ) には、電束を打ち消すに足る負の表面電荷（表面電荷密度）が生じる。

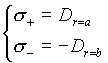(7a)

表面電荷の総和を求めると、(7b)のように表される。

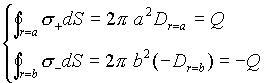(7b)

つまり、同心球の内球面と外球面には、同量逆符号の表面電荷が生じることを示している。

　いま、この同心球面対が角周波数 ω で共振状態にある場合、内球面の表面電荷の総和を Q ( t )とすると、(8)式のように表すことができる。

(8)

電荷の時間変化は電流を表すが、式(3a)より、式(3b)と表される。

(3b)

ここで、 I ( t )は、放射状に流れる電流の源になるものであるので、電荷に対して電流荷と呼ぶのがふさわしい。また I ( t )は Q ( t )と同様、空間的には方向を持たない数値（スカラー）であり、ベクトルではない。

　次に電束密度 D 、および電流密度 J を求めてみるとそれぞれ式(9)、(10)のようになる。

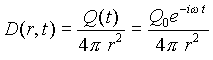	(9)
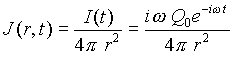	(10)

電束密度 D 、および電流密度 J はともに外向きに放射する方向、すなわち半径方向を正とするベクトルであるが、ベクトルの総和はゼロであり、ゼロベクトル状態である。空間的に特別な方向を持たないのは球対称であるからである。

　電荷と電流荷は位相を90度ずらして共振し、電束と電束電流も位相を90度ずらして共に振動しながら共振回路を形成している。以上をまとめると、表１のようになる。

表１：球対称共振回路の電気振動方程式

電　　　　　　荷
電　　流　　荷
電　束　密　度
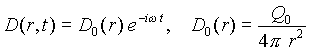電　流　密　度
電束電流密度

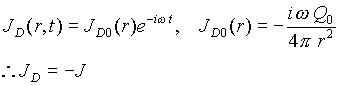　このような共振回路の例にテスラコイルと呼ばれるものがある。テスラコイルでは球状の導体球から糸状の放射電流が観察される。また図６は同心球面対のガラス球面内に希ガスを詰め、放電を起こしたものである。球面間を渦糸状の放電が観察される。この写真から、電流と電束電流がペアになり渦糸状の流れを形成していると考えられる。

図6 球対称の放電場
Fig.6 Discharging current of spherical symmetry.

---