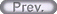２．２　球対称の電磁場

　次に図３のように電荷 Q が時間的に変化する場合を考える。

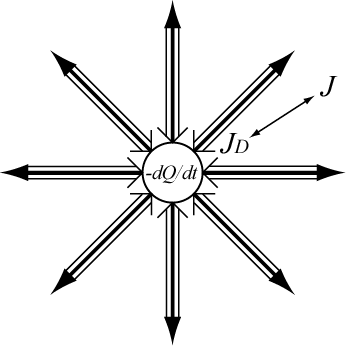
図3　球対称の電磁場
Fig.3 Electromagnetic field of spherical symmetry.

電荷の時間変化は電流を表している。電荷と電流の連続性から、式 (3a) の関係を満たしている。

(3a)

一方、電束密度 D の時間変化は電束電流（変位電流）密度を表している。電束電流密度をと表すと、式 (1b),(2b) から、式 (4) が導かれる。

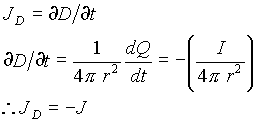(4)

よって、電流密度と電束電流密度は同じ大きさで互いに逆向きであることが分かる。このことは、電流と電束電流がペアになり、球面と垂直方向に往復しながら閉回路を形成できることを示している。前節の直流電流場のように、閉回路を作るために特別の仕組みを作る必要はない。放射された電流は、その同量逆方向の電束電流によって補給され循環しているからである。

　一般に電流が流れると、その周りに磁界 H が生じる。磁界は電束電流によっても生じるが、一般にその関係はMaxell方程式の回転磁界に関する関係式 (5a) で表される。

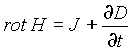(5a)

本節の球対称の電気振動場モデルでは (4) 式で示すように、電流密度 J と電束電流密度は同量で互いに逆方向である（図４）。

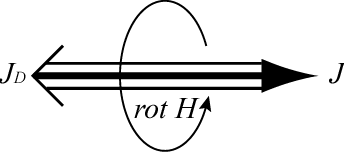
図4　電流と電束電流による回転磁場
Fig.4 Rotating magnetic field both with current and displacement current.

よって (5b) 式が成り立ち、電流の周りを回転する磁界は生じない[2]。

(5b)