2.球対称の電気振動場
2.1 球対称の静電場と電流場
図1のように、導体に電荷 Q が存在するとき、電荷の存在によって静電場が生じる。
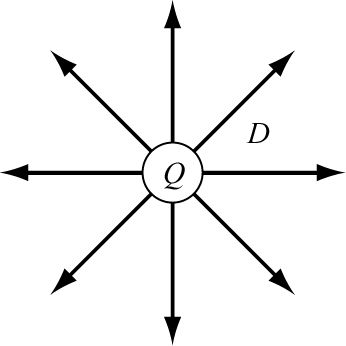
図1 球対称の電束場
Fig.1 Electric flux of spherical symmetry.
電束密度を D とすると電荷 Q との関係は、式 (1a) の関係を満たしている。これは閉曲面を貫く電束の総和は、面内に存在する電荷の総和に等しいことを示しており、一般に電束に関するガウスの法則とよばれている[1]。
|
| (1a) |
図2のように、中心から放射状に電流が流れ出し、電流場を形成している場合を考える。
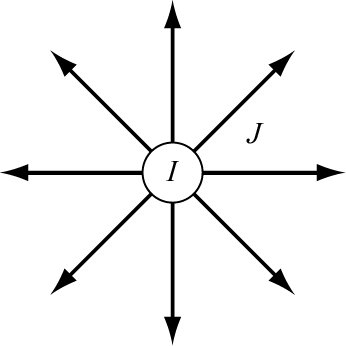
図2 球対称の電流場
Fig.2 Electric current of spherical symmetry.
内側から外側に曲面 S を通過する電流を I 、電流密度を J とすると、式 (2a) の関係を満たしている。式 (1a) の場合と考え方は同じであるが、曲面Sは必ずしも閉曲面である必要はない。実際、直流電流場でこのモデルを実現するには、閉回路を形成する都合上、一部曲面を切り取り、無限遠から中心へ電流を戻して循環させる仕組みが必要であろう。その場合、電流を戻すヘソの部分は除外して積分すればよい。
|
| (2a) |
特に電束分布や電流分布が球対称の場合、電束密度 D 、電流密度 J は中心からの距離 r の関数になる。よって (1a)、(2a) 式はそれぞれ (1b)、(2b) 式で表される。
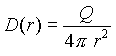 | (1b) |
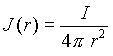 | (2b) |