2. 球対称電気振動場
2.1 電束と電束電流
電束は電気現象を視覚的に表すのに便利である。電束というのは、プラスの電荷からマイナスの電荷に向かう電気力線のことである。電束の出発点にはプラスの電荷が、終点にはマイナスの電荷が存在し、電束が途中で途切れることはない。もし始点や終点に電荷がない場合、電束は無限遠から、あるいは無限遠までのびることになる。電束の定義は、1単位の電荷から1本の電束が出ると取り決めることから、電束と電荷は互いに一対一で対応している。

図1 帯電球と電束
Fig.1 Electric charges and electric flux.
図1は、二つの導体球にそれぞれ、+Qと-Qの電荷を与えたものである。これらは互いに独立しているので、両者の間には電荷の移動はない。また、両者の間にはQ[本]の電束が存在する[1]
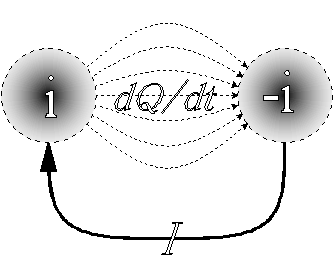
図2 電流と電束電流
Fig.2 Electric current and displacement current.
さて、互いに独立した球の対を、図2のように導線で結ぶとどうなるであろうか。球上に溜まっていた電荷は導線上を移動し、電流Iが流れる。電流は、電荷が単位時間に移動する量と定義するが、電荷Qの量が減った分、電流Iが生じたのであるから、電流Iは、式(1)で定義される。
この導線を流れる電流を実電流ともよぶ。電流には実電流のほかに、変位電流(電束電流)というものがある。変位電流は、電荷の移動をともなわない電流であり、主にコンデンサの電極間を流れる電流である。コンデンサの対向する面の電荷の量が変化することによって、その変化の割合に応じた変位電流が流れる。変位電流は特に電磁波論で重要な役割を果たし、実電流と同等に扱われる。ただ変位電流が実電流と大きく異なる点は、真空中でも絶縁体中でも電流を通すことである。テレビやラジオの電波が、導線のない空中を伝わってくるのは、変位電流の存在があるからである。変位電流は電荷の変化に着目したときの呼び方であるが、電束の変化に着目したときは電束電流と呼ばれる。電荷と電束は一対一に対応しているので、変位電流と電束電流は視点が異なるだけで同じ実体を指し示している。
図2を定常電流による電気回路とみなし、式(1)を式(2)のように変形すれば、閉曲面内に流れ込む電流の総和はゼロであるとするキルヒホッフの法則を表している。