4.3 ＤＥＥＰの複素ポテンシャル表現
従来までの点電荷と異なり，このＤＥＥＰ（複素点電荷）は同一空間（同一点）上に２種類のポテンシャルを持つ．一つは従来の電荷の電位ポテンシャルと同様のものである．もう一つは新たに付加した磁位に相当するポテンシャルで，回転を表すポテンシャルである．つまり複素数で表されるポテンシャルの実部と虚部が，それぞれ発散(divergence)と回転(rotation)を表している．そのそれぞれを発散ポテンシャル，回転ポテンシャルとよび，合わせて複素ポテンシャルとよぶ．
＝（発散ポテンシャル）＋（回転ポテンシャル）
式(8)を式(7)の関係を用いて，実部と虚部に分けると式(10)のようになる．
図４に位相と発散ポテンシャルの関係を示す．位相によって，つまり見る方向によって同じ実体がプラスの電荷に見えたり（位相0度），マイナスの電荷に見えたり（位相180度）することが分かる．つまり位相というパラメータがＤＥＥＰの性質を決める重要な要素になっている．
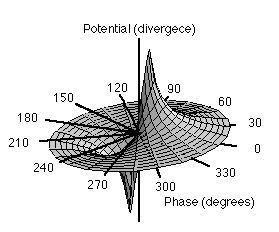
図４ 位相と発散ポテンシャルの関係
Fig.4 Potential (divergence) and phase
位相θがθ＝ωt（反時計回り）あるいはθ＝−ωt（時計回り）で時間と共に変化する場合を考える．時間と共に形状や性質も複雑に変化するが，位相θがそのときの性質や形状を決める．その形状を考察するため，ある位相に着目し，そのときのポテンシャルを表現してみる．これはちょうど対象と同期したストロボを使い，対象の動きを止めてある瞬間だけを撮影する方法と同じ意味を持つ．
実部の発散ポテンシャルの表現は何も難しくない．中心からの距離がｒの位置における高さが単にcos(θ)／ｒだということである．この場合，等高線（等電位面）が同心円状になり，等高線と直交する電気力線が中心から，あるいは中心へ放射状に向かう．
次は虚部の回転ポテンシャルの表現はどうすればよいかである．虚数単位を無視し大きさだけを問題にするならば簡単であるが，それでは回転の意味を表現できない．定性的には，発散ポテンシャルと回転ポテンシャルは互いに直交するので，等高線と電気力線の立場が互いに入れ替わると考えられる．つまり等高線が放射状を向き，電気力線が同心円状を向く．結果的に電気力線が螺旋階段のような渦を巻く場が形成される．
次に定量的に考えるため，虚数部 i sin(θ)／ｒを次のように変形して考える．
2πiｒは複素平面上で半径ｒの円周を反時計回り一周計ったときの距離を示している．そしてその方向に一周回ったときの高さの差が(-2π) sin(θ)であると考え，それが回転の大きさを示しているととらえる．
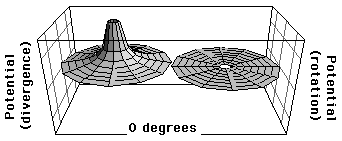
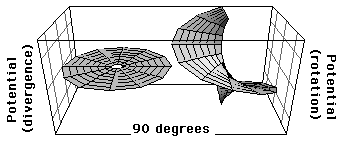
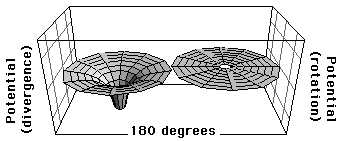
図５は位相をパラメータとして複素ポテンシャルを表現したものである．上から順に位相が0度，90度，180度，270度のときである．またそれぞれの図の左側は発散ポテンシャルを示しており，右側は回転ポテンシャルを示している．図５で，位相が0度のときは，回転ポテンシャルが存在せず，発散ポテンシャルが正の方向にのみ存在することが示されている．これは中心から外部に向かって発散する場を持つ場合で，プラスの点電荷が存在すること同じ意味を示している．また，位相が180度の場合も同様に回転ポテンシャルが存在せず，発散ポテンシャルが負の方向にのみ存在することを示している．これは外部から中心に向かって収束する場を示しており，中心にマイナスの電荷が存在することと同じ意味を示している．
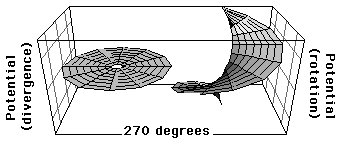
位相が90度と270度の場合は，回転ポテンシャルだけが存在し，発散ポテンシャルは共にゼロである．この状態では従来の意味での電荷は存在しない．つまり電荷としては観測されない状態を示している．しかしこのことは，それが電荷以外の‘何か’として観測されるか，あるいは何ら観測されないかに関わらず，何らかのエネルギーが依然として存在していることを示している．
図５ 点電荷の複素ポテンシャル表現
Fig.5 Complex potential of DEEP
