3.3 数の認識とeiπ=−1の意味
数というのもの歴史をひもといてみると,やはり自然数の発見が最初であろう.英語における人称や,名詞の単数・複数などに見られるように,基本的に人間は,一,二,三,と自然に数えられるものをまず認識してきた.そして順次数えられないものや,負の数やゼロの概念が発見され,表現の自由さや範囲が広がってきたと考えられる.
さて,左から右に向かう水平線を書けば,それを数直線とみなし等間隔に整数をプロットすることができる.その数直線上を有理数や無理数で埋め尽せば,その数直線上の集合は実数の集合となる(図1).
実数の範囲では2乗してマイナスになるような元の数は存在しない.(プラス)×(プラス)も(マイナス)×(マイナス)も共に(プラス)となり,数直線上には2乗してマイナスになる元の数は存在しないのである.ところが,2乗してマイナス1になる元の数があると仮定して,それをiという記号で表すことがある.このiを虚数単位とよび,これも数の仲間入りをさせるように数概念を拡張したのが複素数である.虚(うつ)ろな数という名前の通り,現れては消え,理性では捉えどころのないイメージのような数である.しかし,英語で虚数のことを an imaginary number というように,想像上必要な概念でもある.虚数の定義を数式で表現すると,
である.これをイメージでとらえるために実数(理性)軸と垂直な方向に虚数(想像)軸を描くと図2のようになる.
図1 数直線上の点(直線思考)
Fig.1 Line and number (linar scope)
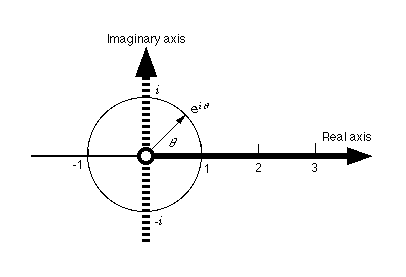
図2 複素平面と単位円(回転思考)
Fig.2 Complex plane and unit circle (plane scope)
虚数をイメージ的実体としてとらえるため,虚数単位‘i’を「原点中心に反時計回りに90度回転させる性質」と定義し直す.i×iは,90度の回転を2回,すなわち原点中心に180度回転させる性質と捉えることができる.i×i=−1は,1を原点0に対して180度回転させると−1になるということを示している.
自然対数e=2.71828...と円周率π=3.14159...と虚数単位iを組み合わせて,負数を表現できる興味深い等式がある.これはオイラーの等式とよばれるもので,
または,
と表現される.
ex は,微分して形の変わらない関数を表しており,虚数iは回転とその方向を表している.つまりeiπという数の意味は,1から単位円上を反時計回りに回転し,距離πだけ進んだときの値を意味している.これが−1であることは,図1の数直線をいくら眺めていても分からないが,図2のように視野を平面に広げ,イメージを加えて考えることによってはじめて式の意味が分かってくる.
次にペアシステムを数学的に表現することを考える.数直線上で考えると1+(−1)=0であるから,1と−1は0を中心としたペアとみることができる.つぎに視野を平面にまで広げると,1とeiπは0を中心としたペアを形成している.
複素平面上の単位円は,実数軸となす角をθとすれば,eiθで表される.さらに三角関数で表現すれば,
と表すことができる.
また単位円上を角速度ωで回転する場合,時間t経過後の角度はθ=ωt で表される.eiωt は,角度ωtの値に応じ,1や−1の値,あるいはiや−iの値とる.eiωt という記号は陽性と陰性,粒子性(位置)と波動性(回転)を表す数学的記号を表している.