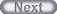3.2 直線コイルのインダクタンス
二つの球面が互いに逆位相で電気的に振動するには、内側の球面と外側の球面との間で電荷の移動がともなわなくてはならない。これをどのように考えるかが問題である。内側と外側を単純に導線で結ぶのが簡単であるが、導線を流れる電流によって磁界が生じるので、その磁界が変位電流の球対称性を崩すことにもなる。誘電体で形成された球形コンデンサの場合は、真電荷の移動がなく分極電荷の生成を考えるだけでよいので、球の対称性を全く損なわない。真電荷の移動を考え、対称性をも問題にする場合は、二つの球面間の空間を乱すことなく両者をつなぐ方法を考える必要がある。もし空間が四次元であれば、内側と外側を両者の対向する空間を通ることなく結ぶことが可能であるが、三次元空間ではむずかしい。それを可能にする方法としては、無誘導型のコイルを使う方法がある。無誘導型というのは、コイルの形(巻き方や空間的構成)を工夫することによってコイルの外側に磁界が生じないようにしたものである。たとえば互いに磁界をうち消すような特殊な巻き方が考えられる。
このような構造体は、電気的には内側と外側の立場が周期的に入れ替わり、内側と外側を区別することができない。位相幾何学的には内側と外側の区別がないクラインの壺と同等のものになると考えられる[3]。
コイルの形状は、共振回路全体の構成に大きく影響を与え、またインダクタンスの値や共振周波数にも影響を与える。ここでは基本周波数を求める都合から、もっとも単純な場合を考える。つまり、単純に両者の間を電荷の移動ができるような針金状の導電体で結ぶモデルで考えることとし、それによって起こる磁場や変位電流の球対称性からの乱れは無視できるものとして考える。
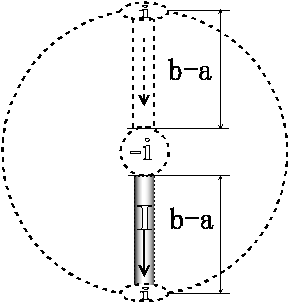
図8 直線コイルのインダクタンス
Fig.8 Inductance of a linear coil.
無限長の針金状の導電体を考える。単位長あたりに蓄えられる磁場の内部エネルギーとインダクタンスの関係、