DEEP model

　電磁気学において、点電荷はもっとも基本となる存在であるが、 その構造をあえて問うことはなされない。 一方、物理学において、点電荷のエネルギー発散問題は未解決の問題として残されている。

　粒子性と波動性、電荷と電流荷、二つの異なる性質を併せ持つ点電荷（→複素点電荷：Dual Essentialities of Electric Pole=DEEP）の存在を仮定する。

球面定在波

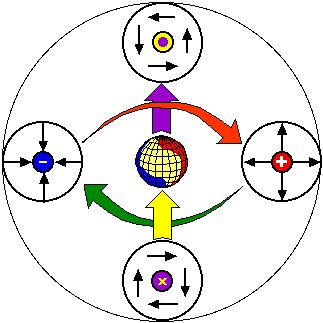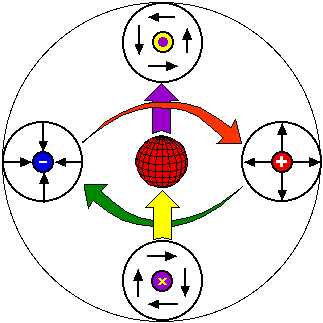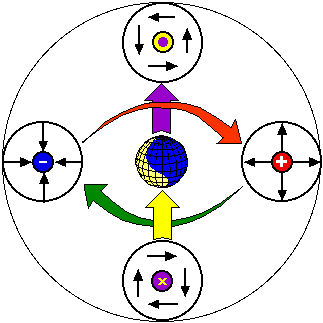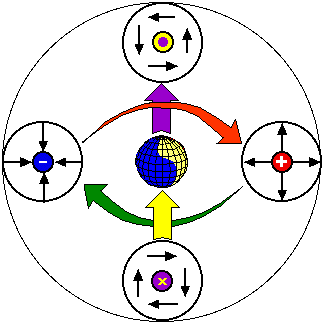
　複素点電荷をポテンシャルの波動として扱ったものが「球面定在波」である。
球面定在波は複素振幅をもち、 実部が電圧・虚部が電流を意味する定在波である。 内径、外径、周波数（波数）、内部エネルギーの間に密接な関係があり、相互にパラメータを規定するという特徴がある。

　球面定在波を電子モデルに対応させる。 電子のコンプトン波長、リュードベリ定数、電子質量、イオン化エネルギー、などの各種パラメータが自然と導かれ、既存の物理定数とも一致する。

同一対象を互いに逆方向のアプローチで研究

A という枠組から B という結論が得られているとする。
結論 B の例外的な現象が見つかった場合、B の反例を仮定して、枠組 A の前提を検証することになる。
論理的に「 A ならば B である」という命題と、その対偶である 「 B でないならば A でない」という命題の真偽は一致する。
片方が正しいアプローチならば、もう一方も正しいアプローチといえる。
しかしながら、同一対象を互いに逆方向のアプローチで研究する研究者同士は、 互いに相手を受け入れ難く感じるであろう。
なぜなら、互いに相手によって自分の前提や結論が否定されるからである。

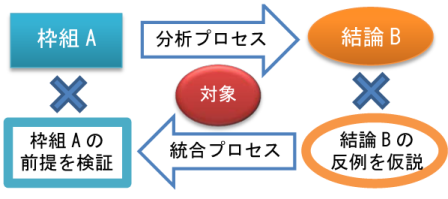
枠組から結論を導く狭義の科学的プロセスを分析プロセスと呼べば、 そのプロセスを逆に辿って枠組を検証するプロセスは統合プロセスと呼べる。
これらはそれぞれ微分と積分の関係に似ている。 積分は微分して対象の関数になる元の関数を探す作業になる。 積分関数は見つからない場合もあるし、 見つかっても積分定数の不確定性も残る。
最終的な目標は、「結論 B」と「結論 Bの反例」の両方ともを満たす新しい枠組を組み立てることである。 つまり、枠組 A を内含する形で拡張することができれば、科学の扱う対象を広げることが可能になる。

「電磁波は横波である」とは，従来の電磁気学の枠組から得られる結論である。
ところが，完全な球対称の球面波では、電界やベクトルポテンシャルの波動は縦波となる。
縦波の存在を仮定すると、電磁気学の前提を見直す必要が生じてくる。
球面定在波のモデルでは、電荷は球面定在波の波源に対応していることが分かってきた。
電荷の意味を問い直し、電荷の定義そのものも見直す必要が生じてくるだろう。

（帝塚山学院大学　戸上 良弘）